内容提要【归纳法和演绎法的区别】热度:57
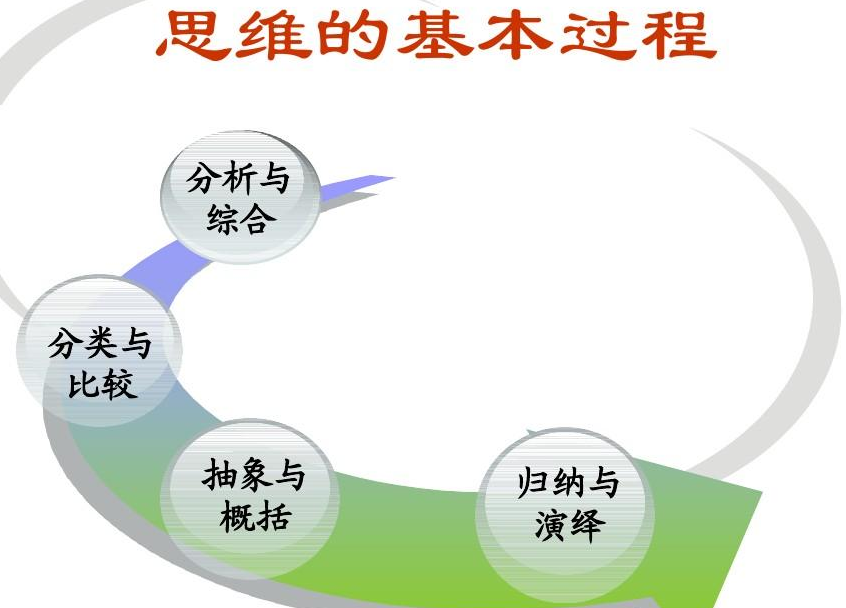
归纳与演绎是相对的。
归纳就是归扰,归结的意思。它可以按
逻辑思维把诸多的条条框框,枝枝节节
归结起来,缩短成主要几条。
它也是一种推理方法。把一系列的具体
事实概括成一般原理。
使纷繁复杂变成简单明了。
而演绎就绝然不同了。它虽然也是一种
推理方法,但它是将一般原理推出成某
种结论。
归纳法和演绎法的区别是什么?
个人觉得,就一般性质上的归纳与演绎法来讲,相辅相成大同小异。按照客观逻辑上,归纳只是由内因而产生的各项数据库和自然条件中发生发现的事物,再进行条文式的总结和归纳罗列出来的一个过程。
演绎法,经过对事物现象的本质,二次分析和研究,客观地演绎出具有崭新的,达到-定高度,可行的科学鉴证的一种演绎过程。她具有大众化,真理化和利益最大化。
此两种方法多用于学术研究和学术论文上面。如:按照马克思唯物主义论的观点,分析总结罗列出了若干个小节,诸如人类科学,自然科学,劳动关系和劳动力再生以及尝试分配关系等等。又如伟大领袖列宁在“十月革命”中的演说,毛泽东主席在革命初期“工人运动”中的演说等等。
高中数学思想方法具体有哪些?
主流的说法,数学思想有四大:函数与方程思想、分类讨论思想、数形结合思想、化归与转化思想.
咦,好像什么行业都有四大?
四大名捕,四大天王,四大会计师事务所,四大名著......额,可能四个好记吧.
一、函数与方程思想
在什么是函数思想谈到了函数思想,方程思想和它算是好吧.
1.是不是想到把给定的等式看成关于某个未知数的方程,是不是想到研究这个方程根的情况.
看一个栗子.
分析:已知和所求差异很大,化简方向不明,求解较困难.如果我们换一个思维角度,把条件看作关于某个变量的二次方程,或许能简化运算.
当然,我相信通过变形、化简也能得到上面的结果,但是不如这样处理来的直接,思路清晰.
2.求解n个未知数时是否想到寻找n个独立的方程?
这也是方程思想的一般体现.
尤其在圆锥曲线综合题中,方程思想体现的淋漓尽致.
圆锥曲线综合题的特点就是几何量多,量之间的关系错综复杂.有人说解析几何就是找关系,道出了核心所在.
在这种情况下,我们希望依次、逐步地把各几何量求解处理是不好实现的.要诀就是建立关于它们的方程,要解几个未知量就要建立几个方程.
二、分类讨论思想
分类讨论思想又分为分类与整合思想.即先对复杂的情况进行分类,然后把各部分的结果整合在一起.
在生活中,大家有这样的体会,有人问你一个很笼统的问题,你无法给出明确的答案.
比如,有人知道我是教数学的老师,就问我:左老师,你每次数学考试都能考100分吗?
我应该如何回答呢?
你要说能,那就太狂了吧;你要说不能,正中提问者的下怀.
于是,我回答:看情况吧.如果总分为150分,我能考100;如果总分为100分,那我考不到.
这里就用到了分类讨论的思想.
解数学题也一样,当解到某一步时,无法用统一的方法,统一的表达式继续往下,因为被研究的问题包含了多种情况.
首先要有分类讨论的意识,其次,要找到分类讨论的标准.
初等数学中,在什么情况下要讨论呢?
比如去绝对值要讨论式子的正负,设直线要考虑斜率是否存在,等比数列求和要考虑公比是否为1,分段函数要考虑代入哪个解析式,二次函数的最值要考虑自变量是否在定义域之内...
三、数形结合思想
在数形结合解函数综合题4,数形结合解函数综合题3,数形结合解函数综合题2,数形结合解二次函数综合题中,我举了很多例子来说明.
四、转化与化归思想
把陌生问题转化为熟悉问题
把多元问题转化为少元问题
把复杂问题转化为简单问题
把立体问题转化为平面问题